Hali
A suliban kaptam egy olyan feladatod h tervezek egy olyan számlálót ami így számol: 0->2->6->9->B->D->F
De sajnos nem voltam az utsó órákon:s
Eddig erre jutottam remélem jó, ha vki tud pls segítsen.
Elöre is kösz

CD4017 es dioda matrix

J-K tárólokkal kéne megoldani

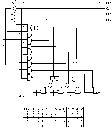
Tessék, egy "elrettentő" példa, már ami az alkatrésztemetést illeti
JK tárolók, ÉS- és VAGY-kapuk, valamint inverterek vannak benne. Az igazságtáblázatban x-ek állnak azokon a pozíciókon, ahol mindegy, hogy az adott vonal milyen szintű a következő lépésnél, mert a tároló kimeneti állapotát nem befolyásolja (pl. egy JK törli a Q kimenetét akkor, ha J = 0 és K = 1, meg akkor is, ha Q = 1, J = 1, K = 1, mert ekkor 0-ra invertál; vagyis, ha éppen tudjuk, hogy Q állapota 1-ről 0-ra kellene, hogy váltson, a 01 és 11 bemenetek is megfelelnek, azaz x1 állhat ott, kevesebb kombinációt kell leírni, egyszerűsíteni).
Ki is próbáltam, működik. Lehet, hogy egyszerűsíthető még, annyira nem volt időm belemélyedni; NAND-, illetve NOR-kapukkal valószínűleg még egyszerűbb volna, de ez már legyen a te házid

Köszi a képet....
azt a részt nem értem h h lesz az igazságtáblából kapcsolási rajz

Az úgy lesz, hogy elkezdi az ember leirkálni a változók egyenleteit, egymás után, és egyszerűsít. Megpróbálom megmutatni, sajnos a negálás hiánya miatt egy kicsit csúnya lesz, de talán érthető (nagybetűvel a ponált, azaz igaz változót írom, kicsivel meg a negáltat, amit felülvonással szoktak jelölni).
Táblázat ugye elkészül, első változónak válasszuk a J3-at. Megkeressük, hol 1 az értéke: egyedül a 6-hoz tartozó sorban. DCBA-ból jön a képlet:
J3 = d & C & B & a (vagyis D nem és C és B és A nem). Ezt nagyon nem lehet egyszerűsíteni, és ha a rajzon megkeresed a J3 (bal szélső tároló J-vonala) vezetéket, akkor egy négybemenetű ÉS-kaput találsz rajta, ami a D és A jeleket invertálva kapja, a B-t és C-t pedig nem; azaz D nem, B, C, A nem.
Vagy pl. a J2-nél:
J2 = (d & c & B & a) + (D & c & B & A), c & B -t (azaz C nem és B) kiemelve egyszerűsíthetünk, ekkor:
J2 = (c & B) & ((d & a) +( D & A)). A rajzot nézve balról a második tárolón van J2, egy ÉS-kapu kimenetén van, annak a kapunak az egyik ága a (c & B) feltétel, a másik ága egy VAGY-kapu, aminek meg két ÉS-kapu van a bemenetén, a (d & a) + (D & A) feltételeket "figyelve", azaz a megfelelő vezetékekre kötve.
Elég nehéz így elmagyarázni, de hátha már kicsit közelebb leszel, a rajzot és a táblázatot nézve hamar rá lehet jönni a lényegre. Biztosan csináltatok BCD-hétszegmens dekódolást, ez ugyanaz az elv, csak nem a hét szegmens vezérlését kell lehuzalozni, hanem a J és K vonalak függvényeit.
Mindjárt utánanézek, van-e erről valami elektronikus anyagom, de félek, csak könyvekben találom meg (tankönyved nincs?).
Ha nem megy, szólj, megpróbáljuk máshogy.

Nem lehet ezt egyszerűbben?

Pl. ha megnézzük, a Q1=Q4 -el, tehát elég az egyiket figyelembe venni, és a másikat csak ugyan onnan vesszük le. (esetleg meghajtva egy-egy pufferrel)
Tehát, ha Q1-et figyelmen kívül hagyjuk, és Q2-t vesszük az első helyiértéknek, akkor azt láthatjuk, hogy a PIROS vonallal jelölt résznél kell egy ugrást belekombinálni (egyszerre kettőt kell léptetni), azon kívűl sima léptetés felfelé.

Azt kellene kilogikázni, hogy a Q4,Q3,Q2 = 0,0,1, akkor kettőt lépjen, hogy a következő állapot 0,1,1 legyen, ne pedig 0,1,0
Egyébként, ha a számolás úgy jönne, hogy 0,2,4,6,9,B,D,F akkor az ugrásra nem is lenne szükség, egyszerűen csak a kimeneteket kellene eltolni úgy, hogy a Q2-t vennénk az első helyiértéknek.

Bocs, nem tudom jobban megfogalmazni, de remélem érthető.

Ha jól emlékszem, mi az ilyen, vagy hasonló feladatokat a suliban V-K táblák segítségével készítettük.

Mindegyik J és K bemenethez egy-egy v-k tábla?
És h kell beírni a vk táblákba az egyeseket?
Melyik helyiértékre melyik kimenetet írjam?

Teljesen érthető, és logikus is, és csak megjegyeznék pár dolgot, nem kötekedem.
Szinkron sorrendi hálózatot kell a kérdezőnek tervezni, én meg a volt előadóimból kiindulva olyat is igyekeztem csinálni. Annál sajnos nincs két lépés egy órajelre; a szinkron hálózat mindig közös és egyazon órajellel léptetett tárolóelemekből, és a bemeneteiket vezérlő logikai részből állnak, annak idején mi is bevetettünk egy-két diódát a sikerért, az egyes után leszoktunk róla.
A Q0-Q3 valóban együtt jár, ez valószínűleg azért nem tűnt fel, mert tegnap reggel 7 óta dolgozom. Jó kifogás, tudom
A puffert még nem keverném bele, nekünk is csak ezt a témát követően kezdtek el fan-out-os problémákat feszegetni, ráadásul a büszkén leadott és elfogadott dolgozatokon szemléltetve.
Azon meg kár gondolkodni, hogy "ha úgy kellene számolni, hogy...", mert nem úgy kell Tantóbácsi megmondta, oszt annyi. Az igazadat ettől függetlenül nem vitatom

Bocsi kobold lehet h én vagyok az értetlen de azt nem látom h az igazság táblájából h jövök rá h hova milyan kaput tegyek, h írjam fel az egyes kimenetek fügvényeit?

Négyváltozós KV-táblát gondolom tudsz rajzolni, az ugye egy 4 x 4 mintermet tartalmazó négyzet. Hagyományosan D, C, B, A jelölésűek a változók, ahol D a legmagasabb helyiértékű, ennek itt most a Q3 felel meg, C = Q2, B = Q1, A = Q0.
Ha azzal megérted, csináld úgy, de ugyanazt az eredményt fogod kapni, mintha megnéznéd a rajzi táblázat egy-egy oszlopát (J3, K3 stb.) egyesével, és az ott található egyesekre felírod a bal oldalon látható, az adott sorban lévő DCBA kombinációt. Ha egy oszlopban több egyes is van (pl. J2, K2), akkor az ugyanahhoz a változóhoz tartozik; az egyik egyesnél is lesz valamilyen DCBA kombinációd ÉS-kapcsolattal (& jel), a másiknál szintén, és ezeket VAGY-kapcsolatba (+ jel) hozva megkapod az adott oszlop változójának a függvényét.

Utálom az egyenletszerkesztőt, de beírtam, mit kellene kiolvasnod a táblázatból.
Beletettem a rajzot is, és egy logikai kapcsolatot külön megjelöltem, hogy lásd, mit jelent a szöveg, hogyan lesz belőle kapu.
Remélem, ez segít valamennyit.
Most látom, hogy van, ahol összeérnek a negálások jelei, a valóságban nem (minden változó egyesével van negálva, nincs olyan, hogy CB egész nem).

Ezer hála a képletekért.
De h megértsem h h jöttek ki ezek ebből az igazságtáblákból felsorolnád nekem a határozatlan értékeket legalább 1 bemenetre.

pl a J3 eseténben 9,B,D,F
csak a határozatlan vagy az összes többi is ami nem szerepel a táblázatban?

Nincsenek határozatlanok, csak olyanok, amik nem számítanak (rendes neve a redundáns változó: értéke tökmindegy, nem befolyásol semmit).
Ha nagyon zavar, az összes x-et cseréld ki 0-ra, merthogy bárhol ugyanúgy jelenthetne 0-t, mint 1-et, csak mi eddig az egyeseket írtuk fel, ezért írj nullát.
Korábban már leírtam, miért jelöltem őket így; ha azzal kapcsolatban van kérdésed, akkor kérnék egy kis pontosítást, mit is írjak még le.

Ha pedig félreértettelek, és te a hazárdokra gondoltál, akkor olyan itt nincs, lévén élvezérelt működés, minden vonal állapota állandósul az órajel lefutó éle előtt, és a szinkron üzemmód miatt egyszerre billen az összes tároló.

Ja, ez a baj... Későn olvastam; a redundánsokról beszélsz. Pl. amikor 9-ről billen a rendszer B-be, J3 lehetne 1, mert akkor beírás történne (K3=0), de lehetne 0 is, mert akkor meg tárolás, azaz nem változik a kimenet állapota; 9-nél az a kimenet 1, B-nél is 1 kell, hogy legyen, innentől tökmindegy, hogy beírunk, vagy tárolunk, azaz JK = 10 vagy 00 kombinációt állítunk be, mert a kimenet ugyanúgy magas lesz.
Ugyanitt, 9-ről B-be esetén, 1x van a J1-K1 vonalakon. 9-nél az a kimenet 0, B-nél már 1 szükséges; ezt vagy beírással érhetjük el, azaz JK = 10, vagy invertálással, mert Q1 = 0, JK = 11 esetén pedig invertálna. Azaz ennél a lépésnél csak annyi a lényeg, hogy J 1-ben legyen, mert akkor akármi van K-n, a Q1 kimenet úgyis 1 lesz az órajel után.

Ha ezt beírnám egy V-K táblába akkor mi kerüljön azokba a négyzetekbe amiknek az értéke nem szerepel az igazságtáblában, azok is "redundáns változó"-k?

Azok szerintem nem redundánsak, hanem tiltottak. Ugyanis kötött a számlálási ciklus, nem is léphet fel másféle állapot, csak az előírtak, különben fagyás lesz... Feltételeztük, hogy a tápfeszültség bekapcsolásakor minden kimenet 0, azaz a ciklus elején állunk, onnantól nincs baj; ha mégis olyan állapot lépne fel, ami nincs benne a specifikációban, akkor a tervező (ez te vagy ) majd előírja, hogy használat előtt az áramkör reset-jét biztosítani kell...
Egyébként nekem nem rémlik, hogy szekvenciális hálózatot KV-táblába rajzolgattunk volna. Lehet, én sem figyeltem oda eléggé, de mintha ez a módszer a kombinációs hálózatokhoz tartozott volna, a szekvenciálisra állapotábra szolgál.

Köszi a segítséget és ezer hála érte

Szívesen.
Nehezen, de csak megszültük

szevasztok!
úgy látom nem csak én fordulok hozzátok ilyesmi segítségért mint tomivontoth osztályátársak vagyunk,és nekem is ugyan ezek kellenének
Megoldható lenne?
Az én feladatom: 0->1->4->8->A->C->D előre is köszi aki segít

Valószínűleg túl bonyolultan magyarázok, ezért nem tudott neked az osztálytársad segíteni.
Na meg mintha nem gondolkodnál önállóan
Tessék, egy szinkron számláló a megadott szekvenciára, Q0 értelemszerűen a legkisebb helyiértékű kimenet.

Nekem ez elég bonyolultnak tűnik, szerintem lehet egyszerűbben is. Később megpróbálom.

hát az az igazság hogy nem fáradoztam vele,van elég sok más dolog is az elektron kívül,matek,irodalom,töri...így érettségi előtt azzal kell jobban foglalkozni,ez csak egy kis kiegészítő ez elektronikában

Na itt az én verzióm. Azok a kapuk, ahol be vannak húzva a bemenetek, azok VAGY kapuk akarnak lenni, csak elfelejtettem bekerekíteni a bemenő oldalukat.

köszi mindegyikőtöknek

A számláló szinkron nem a hálózat... a hálózat sorrendi!

Hello
A suliban a következő hf-et kaptuk és a segitségeteket szeretném kérni mivel még nem vagyok vmi penge a témában:
Szinkron sorrendi hálózat tervezése speciális kódolással. Számlálási irány: hátra. Felhasznált épitőelemek: d flipflop. Egyéb előirások: Bin(16állapot)/BCD(10állapot) előválasztása. Válaszokat előre is köszi!