Hello mindenkinek!!
Kíváncsi lennék,hogy a különböző jelek felharmónikus komponenseit hogyan lehet kiszámítani!!!
Gondolok ilyenekre mint például a négyszög,háromszög,fűrész,lépcsőzetes jelalakokra!!!
Képlet,rajz....bármi jöhet!!!
Ha valaki tud nekem segíteni eme kérdésben akkor nagyon hálás leszek!!

Amire te gondolsz, az a Fourier-transzformáció lehet: tessék. Van benne képlet, ábra, minden.
Nem kifejezetten egyszerű, differenciálást - integrálást oda-vissza vágni kell hozzá, ha tényleg érteni akarod.
Nekünk a fősulin egy 200 oldalnyi jegyzet csak erről szólt... és igazából nem tudtuk megtanulni, csak levizsgáztunk valahogy.

Te jó ég!
Most már értem miért olyan nehéz egy jó rádióadót megépíteni, hogy az ne "fröcskölje" szét az éterben az adását. Ugye erről is szól ez a dolog, vagy ott egyszerűen le kell szűrőzni az al és felharmonikusokat?

Rádió építéséhez (még mindig) keveset tudok Ha jól látom, akkor a sugárzott jel sávszélessége a rezgőkör jósági fokától fog igencsak függeni; minél jobb ez az érték, annál kisebb a sávszélesség, azaz annál erősebben nyomja el (nem viszi át) a vivőn kívüli frekvenciákat. Szűrni - szerintem - jellemzően inkább a vevő oldalán szoktak.
Őszintén szólva, gyakorlati hasznát még nem vettem a Fourier-transzformációnak, kivéve azt, amikor kopogásérzékelő szenzor jelét kellett feldolgozni, és spektrumokat megjeleníteni (de az inkább programozási feladat volt). Fősulin digitális szakirányra jártunk, és szomorúan láttuk, hogy az annyira szeretett négyszögjelünk valójában egy nagy összevisszaság eredménye, de ennyi...
Bocs az off-ért.

Annak idején amikor az fm szintézist leírták a dx7-es kézikönyvben, valahogy úgy írták, hogy a négyszögjel áll egy alapharmonikusból, és végtelen számú felharmónikusból...
Mindenesetre ezt találtam a googlen:
Bővebben: Link

Jobb rádióadóknál 2-3 fokozatú felharmonikus szűrőket alkalmaznak általában.

Akartam is írni, hogy javítson ki, aki ért hozzá, csak elfelejtettem...

Semmi gond... bemenő szűrők is vannak... a jobbak több fokozattal, szintén.

"-Ha jól látom, akkor a sugárzott jel sávszélessége a rezgőkör jósági fokától fog igencsak függeni; minél jobb ez az érték, annál kisebb a sávszélesség, azaz annál erősebben nyomja el (nem viszi át) a vivőn kívüli frekvenciákat. Szűrni - szerintem - jellemzően inkább a vevő oldalán szoktak."

Rádió adó építésnél is a kimenetre antennára kerülő jel tisztasága fogja meghatározni a zavaró sugárzás mértékét. Erre elég szigorú szabályok vannak! A legtöbb adó nem egyszerűen egy oszcillátor + egy erősítő!

Régebben sokszorozással állították elő a vivőt, gyakori szorzók 2x 3x 5x. A módszer egyszerű : egy pl kvarc oszcilátor jelét egy nemlineáris (pl C osztályú) fokozatra küldik a kimenetről szelektíven kiválogatják a kért harmonikust (rezgőkör) majd, újra, + újra, amíg el nem érik a kívánt vivőt. (Mondjuk 8 Mhz kvarc 18 szorozva 144MHz) Itt már Furier bácsi minden elképzelhető filharmonikusa jelen van Ezután szelektív erősítő(k), modulátor és végerősító jön. Ez valamennyit javít a helyzeten ezután a végső szűrés és illesztés jön (gyakran egy PI aluláteresztő) majd antenna.

Természetesen a korszerű(b) berendezések keveréssel vagy PLL rendszerrl állítják elő a vivőt, -gyakran egy lépésben. A jó hatásfok miatt a végfokok ha mód van rá C, D, oztályban működnek (sokszor még csak nem is ellenütemben) a felharmonikusok eltávolítása ekkor is szűrőkkel történik.
Bocs ha kicsit hosszú lett!

Azt elérni, hogy egy adó ne "fröcsköljön" mindenfélét, több helyen elhelyezett szűrőkkel lehet biztosítani. A moduláló jelnél kell kezdeni, meg kell akadályozni, hogy túl magas frekvenciájú moduláló jelek rákerüljenek a modulátorra. Ha FM modulációt használunk, akkor még a frekvencialöket nagysága is beleszól a kisugárzott jel sávszélességébe, azt is egy határ alatt kell tartani. Ha az adó keverőket is tartalmaz (vagy sokszorozókat), akkor a szükségtelen keverési termékeket is ki kell szűrni. A végén pedig a végfok felharmonikusait is szűrni kell. (Alharmonikusok nincsenek, ha a hordozó alatt jel jelenik meg, az abból adódik, hogy különböző nemkívánatos keverési termékek rákerülnek a végfokra.)
Mindezekből talán legegyszerűbb a "vége", vagyis a végfok utáni felharmonikus szűrő megvalósítása. Előtte "minden-mindennel keveredik" (hála Murphy-nek ), azokat a legnehezebb megoldani.

Örülök neki, illetve köszönöm, hogy hosszan írod, mert van mit tanulnom adás/vételtechnikában, csak lassan másik topikot kellene keresni ennek...
Valószínűleg azért nem tudtam az antenna előtti szűrőkről, mert idáig max. távirányítókat javítgattam, és néhány bitet küldözgettem ide-oda, végtelenségig hangolt rezgőkörökkel (azaz sikeres adás után hangolás a legnagyobb hatótávolságig, műszerek híján).

Hello!
Mivel Fourier-transzformáció papíron elvégzése elég komoyl analízis tudást igényel, így azt ajánlom használj programot.
Az Origin nevű program (én 7.5-ös verziót használok) képes egy adatsort fourier analízisssel felbontani.
Ha megvan a függvényed akkor egy hullámhossznyi periódusból számolj ki mondjuk 1024 adatot, írd be a táblázatba. (ezt a program is kéepst megcsinálni, ha beírod neki a függvényt). Majd Analysis menüben FFT

Egy példát is írok. Az A oszlopban "fill column with" "row numbers" ekkor végig beríja a sorokat. Majd a B oszlopban "set column values" és írd be hogy "mod(Col(A),50)". Így egy szép fürészfogjelet fogsz kapni.
Ha most Analysis FFT-re rámész, hagyhatod az alapértelmezett beállításokon, nyomsz egy OK-t. Ekkor kiad egy ábrát. Alul láthatod magát a spektrumfelbontást és felül meg hogy az addigi harmonikusok hány százalékát teszik ki a jelnek.
Természetesen ez egy folytonos ábra, magák a felharmonikusok nem szimpla csúcsok lesznek, hanem van szélességük. Így ha azt szeretnéd megmondnai hogy pontosan mennyi két tag aránya, akkor nem elég a magasságukat összehasonlítani, hanem a területüekt kell, vagyis integrálni kell az alattuk lévő területet (ezt is kéeps a program grafikusan elvégezni).

Ha nagyon nagy adatot használsz (mondjuk az adatok száma egy nagyságrenddel nagyobb a legmagasabb felharmonikusnál), akkor már keskenyek leszenek a csúcsok és szép ábrát ad ki.

megjegyzés:
A program képes sokféle formátumot beolvasni, pl ha egy oszcillszkóp adatsorát eltárolod egy ASCII fájlban, azt is beimportálja és az az adatsort is FFT-zheted.

Szia Lajcsi!

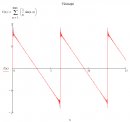
Rajzoltam gyorsan pár fontosabb jelalakot tanulmányaim szerinti képletek alapján, igazából ennyire emlékszem.
A fűrészjel a szinuszok végtelen összege, melyek frekvenciája lineárisan, amplitúdója reciprokkal nő.

A négyszögjel a páratlan szinuszok végtelen összege, melyek frekvenciája lineárisan, amplitúdója reciprokkal nő.

A delta jel (impulzus, tüske) a szinuszok végtelen összege, melyek frekvenciája az 1-hez való különbséggel, amplitúdója szintén az 1-hez való különbséggel nő.

Mire vagy még kíváncsi? Így hirtelen ezek jutottak eszembe, nem néztem utána sehol.

Egyébként a számítástechnikában fontos szerepet tölt be a taylor képlet, amik lehetővé teszi a legtöbb függvény numerikus megközelítését. Tehát egy szinuszt, vagy akármilyen más bonyolult függvényt megközelít egy adott tartományban. Erről sok elemi függvény képére lehet következtetni. Pl. a színusz nem más, mint x/1!-x^3/3!+x^5/5!+..., (ahol a ! a faktoriálist jelenti)

Remélem tudtam segíteni. Üdv. deguss

Nemtudom milyen számitásokról beszéltek,de ne én épitettem már jó pár adót 166Mhz re,174,3Mhz re,legútobb 150mWatt. 17,43Mhz as kvarcal müködött 3,6Volt, 4tranyós +mikrofonerősitő TL272cp volt.Zeneátvitelhez is kiválló hatótáv 850-1500m.Bfr96s Rf.kimenetre kell 5tagúszűrő ami 2tekercs 4-5menet+3kondi.ilyen egyszerű nincs semmiféle sz.gép program.Antenna 3,5menet 10es átmérőn 1,8as huzal+14cm szilikonbev.ú sodrott drót.A szűrő 3-ik,5-ik,12-ik felharmonikust kiszúrte.