Fórum témák
» Több friss téma |
Van egy olyan felírási módja is, csak Te kevered őket.
Tehát kiindulva a kapcsolásból felírt átviteli függvényből: Y(s) = 1/(1+sRC+s^2*LC). Ehhez kell mindig idomítani az átalakított átviteli függvényeket, tehát ha lengő tagként akarjuk felírni, akkor: Y(s) = 1/(1+s*2*kszi*T+s^2*T^2), így kszi = (R/2)*sqrt(C/L) a csillapítási tényező T = sqrt(LC) a sajátfrekvencia. Az a lényeg, hogy akárhogyan is alakítgatjuk az átviteli függvényt, annak mindig egyezni kell ekvivalens átalakítások után a kiindulási átviteli függvénnyel.
Már sok anyagot találtam róla , de mindig másból indulnak ki.Tiszta káosz van a fejemben.Még ha egytárolós lenne , azzal boldogulnék.
Üdv!
A behelyettesítést w=100 rad/sec sikerült megcsinálnom. De a Ta és Tb kiszámítása sehogy sem akar kijönni, ahogy neked. Illetve ha kijön az egyik, a másik már nem lesz a Tiéddel azonos. Mi lehet a baj? Ha meghatároztam a 2 töréspontot , ugye a közelítő Bode -diagramhoz meg kell határozni a decibel és a szög értékeket . Megpróbáltam már, de nagyon rossz eredmények jönnek ki. Valamilyen segítséget tudnál adni?
Itt a próbálkozásom a Ta és Tb kiszámítására.
A csatolt képen elkövettél egy hibát: amikor behelyettesíted a 100 rad/s értéket akkor a másodfokú tagnál a j az négyzeten van (nálad nem), tehát j^2 = -1-szeres szorzó.
A Ta és Tb kétváltozós egyenletrendszer, másodfokú megoldóképlet segítségével számolható. Ellenőriztem, nálam jó. Ha a két időállandó megvan, abból meghatározható a két töréspont az egytárolós tagokra. Azok aluláteresztő jellegűek, a töréspontnál magasabb frekvenciákon -20 dB/dekád meredekségekkel. Ebből könnyen úgy rajzolható fel az eredeti átviteli függvény Bode diagramja, hogy fogod a két függvényt, egymás alá felrajzolod, majd összeadod a két ábrát. Ez a nagy előnye a logaritmikus skálázásnak, hogy a szorzást összeadássá, az osztást különbségképzésre transzformálja (lásd logaritmus azonosságok).
Már a második sor hibás!!!
Ta = R*C-Tb lenne helyes.
Sikerült megcsinálni a Bode - diagramot (szerintem).Elfogadható?
A töréspontokat , hát megint nem sikerült kiszámolni , belekavarodok mindig  . .
Jónak néz ki, de korábban már feltettem a feladat bode diagramját. Az az etalon, ha ahhoz hasonlót sikerült kihozni, akkor jó.
Hasonlít rá.
Töréspontoknál a 2 változós egyenleted ilyen? Tb^2-10^-3TB+10^-6=0 , nekem ilyen.
Ha az L = 1mH, C = 1 uF, akkor az utolsó tag nem 10^-6, hanem 10^-9.
Tehát: Tb^2-10^-3Tb+10^-9 = 0
Üdv!
Sikerült megoldanom a másodfokú egyenletet.Most már nekem is megvannak a töréspontok. Még lenne itt kérésem . Az átmeneti függvény egységugrására adott válaszfüggvénnyel kapcsolatban. Be kellene helyetesíteni xbe*U(t)= 50 1/s -nál.Én ezt megcsináltam .De nem tudom , hogy jó e?.
Na mégsem sikerült megoldani az egyenletet.
 Így így számolok.
Azért ez már nem szabályozástechnikai, illetve villanytani probléma. Kicsit jobban figyelj oda, mert ez már csak arról szól, hogy be tudod-e gépelni a számológépbe a számokat.
Egyébként négyzetgyököt vonva nem az az eredmény, ami nálad van leírva, tehát nem 9,79*10^-4, hanem 9,98*10^-4. Az átmeneti függvényt úgy számoljuk, hogy az egységugrás Laplace transzformáltjával (1/s) kell szorozni az átviteli függvényt, majd inverz Laplace transzformálni kell, így megkapjuk az átmeneti függvényt.
A rendszer egységugrás gerjesztésre adott válaszát az időtartományban a csatolt képen láthatod.
Akkor nem jól csináltam a transzformációt?
Nem tudom, hogy már megint mit keres a nevezőben a 2kszi. Az, ha ilyen formában írod fel, ahogyan tetted, akkor nem kell.
Másik: Ez nem átmeneti függvény amit számolgatni próbáltál, hanem csak a kezdeti és a végérték. Neked most akkor mit kell számolnod?
Ja bocs .A kezdeti és végértéket kell kiszámolni , amikor az egységimpulzus függvény xbe(t)= 50 1/s. Laprance- transzformáció segítségével kell meghatározni.
A másodfokú egyenlet egyik tagja tb2= 10^-6 és tb1=10^-4.Na eddig ok. Sikerült nekem is kiszámolni (végre). Na de, tovább visszaírom a 2. egyenletebe a 10^-6 ott jó ,mindkét oldalt kijön a 10^-9.De az elsőbe nem akar.Tudom nem szabályzástechnikai hiba ,én hibám de akkor se jön ki.
Már megint keveredés van. Most egységimpulzust írsz, eddig egységugrásról volt szó. Gyanítom, csak elírás.
Egyébként a kérdés is kicsit értelmetlen, ugyanis az xbe(t) = 50*1(t) és ennek a Laplace transzformáltja az Xbe(s) = 50*(1/s). Nemde? Nem tudom mi ezzel a probléma. Így kell meghatározni a kezdeti- és végértéket: kezdeti: 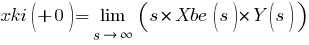 végérték: 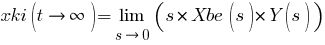 A megadott képletek alapján végzett számítások szerint a kezdeti érték 0, a végérték 50.
Tb2 = 10^-6, a Tb1 = 9.99*10^-4 és nem 10^-4.
Szerintem sikerült megcsinálni az egyenletrendszert.

Úgy érzem sikerült a feladatot megoldani. Persze segítség nélkül nem ment volna.
Köszönöm a türelmed és fáradozásod. 
Sziasztok!
Tudna nekem valaki segíteni? Kaptam egy 5 feladatból álló házit és csak a felét tudtam megcsinálni. Minden segítséget nagyon köszönök. Beszkennelem amit megcsináltam a feladatokkal együtt. Amit kicsikartam magamból az sem bizots hogy jó!
Sajnos nem haladtam semmit a házimmal. A frekvencia függvényemmel lehet valami gond. Lehet hogy egyszerűsítenem kell, vagy valahogy átírni más formába, de lehet hogy egyáltalán nem jó úgy ahogy van?
(1+j*ω*T)/(1+2*j*ω*T)=Y(j*ω) Egy Bode és egy Nyquist diagrammot szeretnék összehozni.
Próbáltam "sany" álltal küldött feladatban levezetett w(s)-t kiszámolni. Nekem ez jött ki: csatolom
|
Bejelentkezés
Hirdetés |
















