Fórum témák
» Több friss téma |
Üdv Nektek!
Már napok óta böngészem az internetet, de nem találok választ, ezér tfordulok hozzátok! Irányítástechnikai tagok műveleti erősítővel való megvalósításáról keresek feljegyzéseket. -Különbségképző és összegző tag -arányos, késleltetésmentes tag -egytárolós arányos tag -ideális integráló tag -ideális differenciáló tag -egytárolós diff. -kéttárolós diff. -PID szabályozó Ezekre lenne szükségem, legalább a kapcsolási rajzukra! Ha valaki tud segíteni, előre is köszi!
Ezt próbáltad a Googleval? "műveleti erősítő alapkapcsolások"...néhány kérdésedre választ kapsz.
igen, próbáltam, és sokmindent találok ,csak az a baj, hogy egyikhez sincs odaírva pontosan az az elnevezés, amiket én írtam, ezért fogalmam sincs, melyik melyik, mivel totálisan hülye vagyok hozzájuk
 Estleg segíthetnél egy picit még, köszi!
Bővebben: Link
4.7 ábra: összegző tag 4.8; 4.10 ábra: különbségképző Bővebben: Link 7 ábra: összegző tag 8.ábra: különbségképző 9. ábra: differenciáló tag 10. ábra: integráló tag. Ideális, ha az alkatrészek is azok. A 4. és az 5. ábra szerintem az arányos tagoknak felelnek meg. Egy PID szabályzó ezen tagok kombinációja párhuzamosan, majd összegezve, de erről szóljon inkább egy irányítástechnikus.
Üdv mindenkinek!
Tudna valaki abban segíteni , hogy a megadott irányítási tagban hogyan kell meghatározni a frekvenciafüggvényt, és az átviteli függvényét? Nagyon fontos lenne. Nem a megoldás kell , hanem csak segítség a megoldáshoz. A válaszokat előre köszönöm!
A WM1 a bemenőjel.A WM2 pedig a kimenőjel.
Hogyan tudnám felírni ebből a frekvenciafüggvényt?
Szia!
Mi a gond? Eddig amit csináltál az helyes. Innen már csak matematikai átalakítások sorozata, hogy olyan alakra hozzuk az átviteli karakterisztikát, melyből le is tudunk olvasni bizonyos dolgokat. Nem tudom ismeretes-e számodra a komplex frekvencia tartomány (s-tartomány, Laplace tartomány) fogalma. Én pl. ebben szeretek számolni, mert nem zavar a sok jw tag. Gyakorlatilag az s = jw helyettesítéssel élünk (elméletben ez kicsit más, mert az a megkötés, hogy a gerjesztésnek belépőnek kell lennie, de ez most nem releváns). Az átviteli karakterisztika W(jw) = Uki(jw)/Ube(jw). Az átviteli függvény W(s) = Uki(s)/Ube(s), látható, hogy s = jw helyettesítést használunk. Kiszámoltam neked a végeredményt: 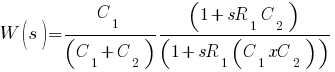 (A C1 x C2 a replusz művelet). (A C1 x C2 a replusz művelet).Azért jó ezt az alakot használni, mert könnyű belőle az aszimptotikus Bode- diagramot felvenni. Az átviteli karakterisztika ebből a jw = s helyettesítéssel kapható meg. Az amplitúdó karakterisztika az átviteli karakterisztika abszolút értéke, míg a fáziskarakterisztika: fi(w)= arctg(Im[W(jw)]/Re[W(jw)]).
Volt némi ráérős időm, gondoltam megmutatom, hogy nagyjából helyes eredményre vezetett a képlet. Az ellenőrzést egyrészt a kapcsolás Multisimben való szimulációjával, másrészt a képlet MATLAB segítségével történő ábrázolásával végeztem.
Köszi szépen az eddigi fáradozásod!
Az nagy kérés lenne , hogyha leírnád hogyan is jött ki ez a végeredmény? 
Most sajnos nem érek rá, de holnap este beszkennelem.
Azért próbálkozhatnál a megfejtéssel, mert igazán úgy lehet fejlődni, ha az ember megküzd az ilyen feladatokkal.
Azt nagyon megköszönném , ha megtennéd.
Már próbáltam ,de sajnos sehogy sem akartak kijönni a megfelelő tagok.
Szia!
Csatolmányban a kérdéses levezetés!
Üdv!
Lenne itt még két kérdésem hozzád ha nem gond. 1.Kérdésem: A tag frekvenciafüggvénye W(jω) =... tag lesz? 2.Kérdésem: Ha megvan adva ω=100 rad/sec , és a tag erősítésének az abszolút értéke a kérdés.Akkor ugye a frekvencia függvénybe kell behelyettesíteni , az ω értékét , a kapott eredménynek pedig a 20logx kell venni?
Szia!
1.Így van, a tag átviteli karakterisztikája (frekvenciafüggvénye) a W(jw). 2. Nem teljesen. Közvetlenül az átviteli karakterisztika nem hordoz valós fizikai mennyiségeket (gyakorlatilag csak egy komplex függvény). Ennek abszolút értéke az amplitúdó karakterisztika, arcus tangense pedig a fáziskarakterisztika (ahogyan azt már korábbi hozzászólásomban leírtam). Ha a két karakterisztikát a logaritmikus frekvencia függvényében, az amplitúdót dB- ben, a fázist fokokban ábrázoljuk, akkor megkapjuk a tag Bode- diagramját. Amikor egy adott frekvencián megkérdezik az erősítést, akkor az átviteli karakterisztika abszolút értékének kell a 20*log10 logaritmusát (így lesz dB) venni (log10 = tízes alapú logaritmus).
Akkor tehát legegyszerűbben a Bode - diagramból tudom leolvasni az erősítést?
Azt kitérőnek szántam, hogy lásd az összefüggéseket. Persze ha már megvan a Bode, akkor onnan is le lehet olvasni, viszont amennyiben nincs meg, akkor az átviteli karakterisztika abszolút értékének meghatározásával, majd w behelyettesítésével számolj.
Üdv!
A megoldást végül időállandók segítségével oldottam meg a frekvencia függvényt felhasználva.Megnéznéd, hogy jól csináltam -e meg? A bode - diagramról amit készítettél, körülbelül ezt az erősítést lehet leolvasni.
Szia!
Nem lesz ez így jó. Mondtam, hogy az amplitúdó karakterisztikát az átviteli karakterisztika abszolút értékeként számítjuk. Gőzöm sincs, hogy Te mit csináltál a feltöltött doksiban (addig jó, amíg nem kevered bele a /j=-1 dolgot. Ezt nem tudom miért csináltad.). Nálam az eredmény w = 100 rad/s esetén abs(W(j100))= 0,5018, ami decibelre átszámolva -5,98 dB. Nézd csak meg a bode- diagramot, amit korábban töltöttem fel. Ezen doksi 5. oldalát ajánlom tanulmányozásra, komplex szám abszolút értékének számítása.
Nálam valamiért nem akar bejönni a csatolt dokumentum.
Ezt jól benéztem , akkor lehetne -1 -et írni , ha j2(négyzet) lenne ott.Ezért írtam -1 -et. Az emlékeim szerint a a valós rész négyzete és a képzetes rész négyzete a gyök alatt az abszolút érték.
Igazán nincs mit, szívesen segítettem. Néha nekem is jól jön egy kis agytorna, nehogy elfelejtődjenek ezek a dolgok.

Hello!
Megint zavarlak a feladatommal ha nem gond.A törtvonalas Bode-diagramját szeretném megcsinálni a feladatomnak.Már csináltam egy-két dolgot.Csatoltam a képet.De sajnos nem akar sikerülni a dolog,nagyon rossz eredmények jöttek ki.Ebben még tudnál nekem segíteni?
Jó estét mindenkinek!
Újra kérdeznék egy feladattal kapcsolatban. Az átviteli függvényt és a frekvencia függvényt már meghatároztam. Ez egy aranyos kéttárolós tag. /nem tudom, hogy jó e./ Nagyon furcsa eredmények jöttek ki. Meg kellene határozni az omega abszolút értékét 100 rad/sec helyen.Megpróbáltam meghatározni, de nem tudom jól csináltam e meg. Kérem valaki ellenőrizze le, ha tud segítsen. Nagyon fontos lenne. Segítséget nagyon köszönöm!
Az első oldalon levő számítások helyesek, tehát kszi = 15,81; T = 3,1623*(10^-5) s. Viszont az abszolút érték számítása biztosan hibás. A helyes, pontos eredmények w = 100 rad/s mellett: |Y(jw)| = 0,9950, ez decibelre átszámítva: -0,0431 dB.
Ha belegondolsz, ez egy kéttárolós tag, melynek nagy a csillapítása (nincs kiemelése az w0 frekvencián) és a törésponti frekvenciája 31623 rad/s. A 100 rad/s ennél jóval kisebb, tehát 0 dB körüli eredmény várható. A csatolt képen az átviteli függvény Bode diagramját láthatod.
Már vagy 2 -szer próbáltam kiszámolni a w = 100 rad/s helyet,de nem sok sikerrel.Különben az úgy jó , hogy kettő törtfüggvényre vettem a frekvencia függvényt ? Mert próbáltam az eredeti frekvencia függvénnyel is kiszámolni szétbontás nélkül. De úgy sem jött ki -20,82 dB lett az eredmény.
Közelítő Bode -diagram is kellene .Elkezdtem csinálni. A töréspontokat kiszámoltam ,de Te a hozzászólásodban azt írtad, hogy csak egy töréspontja van a függvénynek .Miért csak egy töréspontja van? Annyit tudok, hogy a tag viselkedése a szki értékétől függ. Ha a szki > 1 akkor felbontható törtfüggvényre a frekvencia függvény.
Azt nem mondtad, hogy kell az aszimptotikus Bode is. Én a rezonanciához tartozó időállandót adtam meg, azt jelöltem T-vel. De ezt most hagyjuk.
Két törtfüggvény szorzataként felírva is ki kell, hogy elégítse az eredeti egyenletet. Tehát [1/(1+sTa)]*[1/(1+sTb)]-re felbontva a Ta ill. Tb időállandókra az alábbi feltételeknek kell teljesülniük: Ta+Tb = R*C Ta*Tb = L*C, ezt az egyenletrendszert kell megoldani a Ta-ra valamint Tb-re, ekkor kapod a két töréspontot. Nálam: Ta = 10^-6 s -> wa = 10^6 rad/s és Tb = 10^-3 s -> wb = 1000 rad/s. Ha ránézel a korábban feltöltött pdf-re, egészen hihetőek a számolt értékek. Egyébként a 100 rad/s- hoz tartozó amplitúdó értéket az alábbi átviteli karakterisztikából számoltam (komplex számok abszolút értéke): Y(jw) = 1/(1+jw*RC+ (jw)^2*LC) |
Bejelentkezés
Hirdetés |