Inkább kerülném a filozófiát, és fejben már azon gondolkozom, hogy milyen algoritmusokat használjak az MCU-n a mintázatok felismerésére.
A panel majd elkészül valamikor... a kapcsolás tesztelésére sem volt időm, csak megterveztem, és remélem sikerül majd működésre bírni. (a részegységeit sem teszteltem igazán)

A korábbi zajgenerátorom más felépítésű volt, mint amilyen a mostani lesz. Akkor arra próbáltam törekedni, hogy minél jobb, minél egyenletesebb eloszlású bithalmazt kapjak, és persze a kéznél levő alkatrészekből építkeztem. Sok mindent kipróbáltam - és tök jó, egyenletes eloszlású bithalmazt kaptam... de nem ez volt a fő cél, hanem hogy a tudati ráhatást bizonyítsam vagy cáfoljam. Az akkori eredmény a cáfolathoz állt közelebb.
Azt hogy miért vettem elő újra, már leírtam. Több bithalmaz kell (minimum 4...8 halmaz) és az ezek közötti összefüggéseket kell kimutatni, vagy cáfolni.

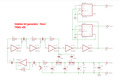
Legyen egy kis elektronika is itt, ezért megosztom az első véletlen generátorom rajzát. Érdekessége, hogy hangszórón meghallgatva, mindhárom kimenet ugyanúgy szól, nem lehet meghallani a különbséget. Viszont a kettes osztás biztosítja, hogy garantáltan (nagyon sok minta esetén) 50%-ban kapunk 0 és 1 bitet, azaz 50% valószínűséggel. Az alap kimenet sem rossz ebből a szempontból, de nem teljesen pontos, azaz egy bolha hajszálnyit eltérhet az 50% valószínűségtől a 0/1 bitek aránya.

Csak egy megjegyzés, ha már feldobtam: Wolfram elmélete nem _úgy_ filozófia. Azt bizonyítja be teljesen földhözragadt reál módszerekkel (: -), hogy nagyon egyszerű kezdeti feltételekből is hatalmas bonyolultság alakulhat ki, ami szerintem óriási jelentőségű, mivel még kevésbé kell intelligens tervezésről meg hasonlókról beszélni. Pl. egy nagyon egyszerű algoritmus ("Rule 110" celluláris automata) is képes univerzális számítást végezni, vagyis tetszőlegesen bonyolult viselkedést produkálni. Nagyon érdekes.

Aki látott már fraktálképeket, és megnézte a hozzá tartozó matematikai függvényt, az egyből belátja ezt. A csatolt képeken a formula: z²+c függvény iterációja.
A programban tetszés szerint nagyíthatók a függvény része, és gyakorlatilag végtelen nagy mintázatot kapunk aminek a részei hasonlóak ugyan, de mégis mindegyik kicsit más...

Még képek...

Szerintem ez messze nem ugyanaz, a fraktálnak nincs számítási és viselkedési komplexitása, változatosságában is ismétlődő és statikus, hoz is valamit meg nem is, mint a mesében. Csodálható, de nem alkalmas logikai műveletekre, számításokra - a Wolfram-féle modellben viszont valódi bonyolultság van. De ne higgy nekem, nézz utána egyszer, amikor kedved lesz hozzá.

Bizony, ami megdöbbentő, hogy a Föld gravitációját már cm-es pontossággal tudjuk mérni az új generációs atomórákkal.
Konyhanyelven fogalmazva, csináltak kísérletet, melyben ezt az órát lejjebb rakták pár centivel, és lassabban járt.

Köszönöm a korrekciót, természetesen nem haragszom.
Pontosabb lett volna, ha odaírom, ez a "nincs" nem saját véleményem, hanem amolyan műszakias, materiális kijelentés. A téma eléggé érzékeny terület, ezért nem egyszerű kijelenteni bármit is határozottan.
De nem is ezt szerettem volna feszegetni.
Próbálom másként.
Egy hangya nem képes felemelni egy pénzérmét, ergo nem tudja meg se fordítani azt. Tehát ha egy hangya úgy akar üzenni nekünk hogy az érme szándékosan valamelyik előre meghatározott oldalán feküdjön, az nem fog neki menni. Viszont nem zárható ki, hogy a levegőben pörgő érmére olyan irányú erőt fejtsen ki, hogy az nagyobb valószínűsséggel essen ugyanarra az oldalára.
Olyan gyenge hatások mint amilyet az elme, vagy amit egy feltételezett alternatív világból üzenő küld nekünk, lehet olyan gyenge, hogy egyetlen kvantum állapotát sem képes megváltoztatni. Viszont ha találunk olyan véletlenszerű eseményt aminek eloszlását ezek a feltételezett kvantum szint alatti hatások el tudják tolni, akkor mégis lehetséges az, ami túlmutatna a fizikai valóságon.
Azt is tudjuk, hogy a kvantum szint alatt nincs semmi, mint ahogy a hangya sem tud megmozdítani egyetlen pénzérmét sem.

Nem véletlen, hogy nincs véletlen.

Nagyon érdekes kapcsolás.
Az RT és HE újságokban is sok kapcsolás volt található. Pl. véletlenszerűen villogó LED, ott három Schmitt-trigger kapu volt.

Egyébként szépen leírtad, hogyan működik a DSP-ben levezetett és alkalmazott eljárás, amikor egyenletes zajt keverünk a bemenethez és túlmintavételezéssel az A/D átalakító lépcsőinél nagyobb felbontást érünk el így további információt nyerve mindabból, ami bemegy az áramkörbe, vagyis a ditherelést. : -)

Itt a lényeg ez lenne hogy valódi véletlenszámot állítsunk elő. Tehát pl. egy mikrovezérlőn használt rnd függvény (általában) egy olyan matematikai függvény ami összevissza értékeket ad, és a rendszeridővel inicializálják. Ez úgynevezett ál-véletlen számot generál. egy játék dobókockához, ruletthez stb. teljesen jó, mert kb. megjósolhatatlan , hogy mil esz a következő érték. Viszont lesznek benne mintázatok, ismétlődések, azaz bár egyenletes, de nem tökéletesen véletlenszerű a számok eloszlása. A TRNG (true random number generator) valamilyen quantum hatásra épül, ami teljesen véletlenszerű, mint pl. radioaktív elemek bomlásakor kilépő részecskék. Persze nem egy hobbi eszköz, sokkal egyszerűbb pl. félvezető-átmenet zaját felhasználni. Pl. egy zener diódában a potenciál-gáton átugró elektronok, vagy elektroncső anódjába becsapódó elektron ami több másikat kiüt a becsapódáskor, és ezek újra becsapódnak az anódba, vagy a segédrácsba.
Az elmélet szerint a valódi véletlen generátor kimenetén nincsenek felismerhető mintázatok, semmiféle összefüggés nem mutatható ki, a korábban generált értékek, és az ezután következők között. Minden egyes bit előfordulásának, kizárólag a valószínűsége ismerhető.

A véletlenszerűen villogó led esetében különböző frekvenciájú oszcillátorok közötti kölcsönhatás (v. interferencia) eredménye adja ezt a hatást, ami jól nézhet ki, de nem valódi véletlenszerűség, csak ránézésre hasonló ahhoz.

Csak annyi kell még hozzá, hogy ennek a zajnak a spektruma ne tartalmazzon hallható sávba eső összetevőket*, és akkor nem ront a jel/zaj viszonyon sem, sőt az amplitúdója ekkor lehet 1 bitnél, ill. 1 lépcsőnél jóval nagyobb is.

*sőt célszerűen olyan összetevőket sem tartalmazhat, ami a mintavételezési frekvenciával kombinálva esne a hallható sávba. Azaz nem sima fehérzaj kell, hanem megfelelően sávhatárolt, és az adott feladatra optimális zaj.

Igen, és az előbb elfelejtettem azt a kevésbé hatékony, de működő esetet is, amikor elég zaj van a bemeneten ahhoz, hogy ne kelljen külön hozzáadni. De én inkább rádióvevőkben, mérőműszerekben szoktam gondolkodni, nem hangfrekiben, bár nincs túl nagy jelentősége. : -) A kvantumos analógia nem tudom, mennyire lenne precíz.

Az álvéletlenszám-generátorokról jut eszembe, csak érdekesség és nem mai cucc: https://www.math.sci.hiroshima-u.ac.jp/m-mat/MT/SFMT/index.html

Hogy ne offoljam a témát, próbálok közel maradni a véletlen számokhoz.
Ha egyetlen mintát veszünk ami két állapotot vehet fel, akkor logikai szintekkel felírva 50/50% az esélye, hogy vagy L, vagy H szintet kapunk. Ha már megtörtént az egyetlen minta elemzése ami mondjuk H, akkor 100% valószínűsséggel H lesz, 0% valószínűsséggel L.
Tehát egyetlen minta nem hoz értelmezhető eredményt.
Ha nagyon sok mintát vesszünk, akkor még több, de nem végtelen lehetőséget kapunk, amit ha már rögzítünk, akkor az stabil, befagyasztott eloszlást fog mutatni. Ha a minták megfigyelését nem hagyjuk abba, hanem nagyon sokáig hozzáadjuk a kezdeti mintához, akkor a variációk száma a végtelen felé fog tartani, de elérni azt nem fogja soha. Viszont egyre finomabb lesz az eloszlás.
Itt kicsit kitérnék, hogy megemlítsem az A/D átalakító felbontásával növelésére tett kísérletet.
Talán fizikailag először egy 8 bites zenekari effektet próbáltunk feljavítani. Az ugye nem kedvező, hogy 8 biten a dinamika csak hajszálnyira több mint 40dB. Elég hamar vagy szaturáció, vagy az alacsony felbontás miatti jeltorzulás volt a jelenség. Az elmélet a következő lehetőségekben próbált megvalósulni:
A bemeneti analóg jelhez (még a S&H előtt) hozzáadni egy négyszögjelet, aminek frekvenciája 1/2 mintavételi frekvencia és szinkronban van azzal, nagysága pedig fél lépésköz. Ez 8 bitről 9 bitre növelte a felbontást, a dinamikát pedig 46 dB-re.
Másik variációban nem négyszög, hanem fűrészjel lett hozzáadva, a mintvételi frekvencia negyedével, szintén szinkronizálva.
Harmadik megoldás a szűrőzött zaj volt, ez maradt is.
Sajnos volt egy korlát. Mivel az A/D konverter lépésközei nem voltak tökéletesen egyformák, nem lehetett a végtelenségig növelni a felbontást. Pedig a mintavételi frekvenciában még volt tartalék. Egy bites szigma/delta átalakítóval talán lett volna még lehetőség.
Nos eme kitérőt azért említettem, mert a véletlen szám generálás is beleütközhet olyan hibába, ami meghiúsítja az egyenletes eloszlású spektrumkép létrehozását, ezzel az olyan kísérlet, mint a gondolat ráhatása egy véletlen esemény kimenetelére, értelmét veszti.
De lehet, hogy csak további finomításra van szükség.
Hozzáteszem, hogy alacsonyabb felbontású és primitívebb véletlen (álvéletlen) szám generátor használata adhat olyan téves eredményeket, hogy azt hihetjük, hatással vagyunk a véletlen esemény kimenetelére.
Erre tudok példát mondani.
Több mint 40 éve a helyi bisztró előcsarnokába betelepítettek néhány elektronikus rulett pénznyelő automatát. Az egyiken felfedezni véltem valami szisztematikus viselkedést. Elhatároztam, hogy eljátszok rajta 200 Forintot, de szigorúan csak egy napig. Azóta sem nyúltam soha ilyen gépekhez, mert nem egyeztethető az elveimmel.
Egy mintázat mindig ismétlődött, ezért nem tudtam eljátszani a 200 Forintomat, mert elég hamar megérkezett a sorozat, aminek következtében a (talán 2Ft-os) tétet fel tudtam tornászni 256Ft-ra. Ezt viszont a nagyok mindig meg vették tőlem, aztán vagy duplázták, vagy bukták.
Úgy gondolom, nem beépített sorozatok voltak csak az egyszerű elektronikai miatt történt mindez.

Adott egy 1 bites átalakító, ami tulajdonképpen egy komparátor. A bemeneti jelhez hozzáadunk egy fűrészjelet, és a fűrész felfutása közben veszünk egy csomó mintát. Kapunk egy marék nulla bitet, majd amikor a fűrészjel+bemenet átlépi a komparátor küszöbét, akkor egy másik maréknyi 1-est. Ha elég sok mintát vettünk, és a 0/1 arányt számmá alakítjuk, akkor a végén 1bitnél sokkal nagyobb felbontást kaphatunk. Ez nyilván nem csak 1 biten, és nem csak fűrészjellel működik, hanem szinte bármilyen (de a bementnél gyorsabban változó) jellel, és az adatok feldolgozását ennek a jelnek megfelelően kell elvégezni. (tehát lehetne akár szinuszjel, vagy háromszögjel is hozzáadva, de természetresen zaj is). A hozzáadott jelet persze jól (a feladatnak megfelelően) kell megválasztani, a lineárisan változó jelek (háromszög, fűrész), és a zaj az, ami rel. könnyen (pl. egyszerű átlagolással) feldolgozható.
Sok esetben az A/D konverter saját zaja is jóval nagyobb mint egy lépcső, ezért egyszerű túlmintavételezéssel + átlagolással is növelhető a felbontás. Sanszos, hogy pl. némelyik 10...12 bites szkóp is valójában csak 8 bites, és ezért szerepel a specifikációjában, hogy a 12 bitet csak kisebb mintavételi sebességek mellett tudja.